欧拉解决了著名的自然数平方倒数之和等于π^2/6,如下图所示,这里对证明不做解释,可以自行搜索。
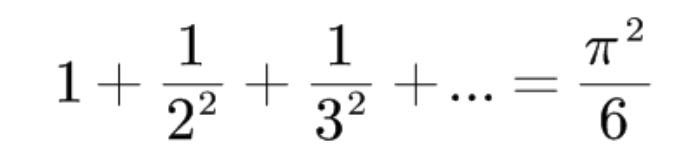
我们直接上代码, 计算π值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
#include <iostream> #include <mpir.h> #include <mpirxx.h> using namespace std; int main() { // π^2/6 = 1/1^2 + 1/2^2 + 1/3^ + 1/4^2 + 1/5^2 + ... mpf_class M; mpf_class P; mpf_class I; mpf_class S; mpf_class N; mpf_class Q; mpf_class D; mp_bitcnt_t prec = 300; mpf_set_prec(I.get_mpf_t(), prec); mpf_set_prec(M.get_mpf_t(), prec); mpf_set_prec(P.get_mpf_t(), prec); mpf_set_prec(S.get_mpf_t(), prec); mpf_set_prec(Q.get_mpf_t(), prec); mpf_set_prec(D.get_mpf_t(), prec); M = 0; P = 0; S = 0; N = "100"; mp_exp_t exp = 0; char* Val; for (I = 1; I <= N; I++) { Q = I * I; D = 1 / Q; M += D; } S = 6 * M; P = sqrt(S); exp = 0; Val = mpf_get_str(NULL, &exp, 10, 0, I.get_mpf_t()); cout << "I:" << Val << endl; free(Val); exp = 0; Val = mpf_get_str(NULL, &exp, 10, 0, P.get_mpf_t()); cout << "P:" << Val << endl; free(Val); cout << "exp:" << exp << endl; } |
当 N = 100 的时候,计算的结果是

上面的exp 表示数点的位置,1位,计算的结果为3.132,接近值为3.1
当 N = 1000 的时候(翻10倍),1千计算的结果是

计算的结果接近值为3.14
当 N = 10000 的时候(翻10倍),1万计算的结果是

计算的结果接近值为3.141
当 N = 100000 的时候(翻10倍),10万计算的结果是

计算的结果接近值为3.1415
当 N = 1000000 的时候(翻10倍),百万计算的结果是

计算的结果接近值为3.14159
当 N = 100000000 的时候(翻100倍),亿次的计算的结果是

计算的结果接近值为3.1415926
其实可以发现,如果每增加一位数字,N就要翻10倍,自然计算量也是翻10倍,这样计算所花的时间是越来越多。