原文参考连接:https://github.com/naklecha/llama3-from-scratch
在本篇文章中,从头开始实现了 llama3,一次一个张量和矩阵乘法。
此外,将直接从 Meta 为 llama3 提供的模型文件加载张量,您需要在运行此文件之前下载权重。以下是下载llama3权重的官方链接: https://llama.meta.com/llama-downloads/
实验是在 Windows 11 环境进行的,使用 jupyter notebook 进行调试
1. 创建 jupyter 环境
|
1 2 3 4 5 |
conda create -n jupyter_env python==3.11 conda activate jupyter_env conda install -c conda-forge notebook conda install -c conda-forge jupyter_core |
1.1 确认 python.exe 路径
|
1 2 |
where python.exe C:\Users\tony1\anaconda3\envs\jupyter_env\python.exe |
1.2 确认 pip.exe 路径
|
1 2 |
where pip.exe C:\Users\tony1\anaconda3\envs\jupyter_env\Scripts\pip.exe |
1.3 确认 jupyter.exe 路径
|
1 2 |
where jupyter.exe C:\Users\tony1\anaconda3\envs\jupyter_env\Scripts\jupyter.exe |
1.4 运行 notebook
|
1 |
jupyter notebook |
2. 安装必要的库
|
1 2 3 4 5 |
!pip install sentencepiece !pip install tiktoken !pip install torch !pip install blobfile !pip install matplotlib |
3. 分词器(tokenizer)
这里不打算实现 BPE 分词器(但 Andrej Karpathy 有一个非常干净的实现)
https://github.com/karpathy/minbpe
可以从 llama3 的 tokenizer.json 文件知道分词器类型是 BPE
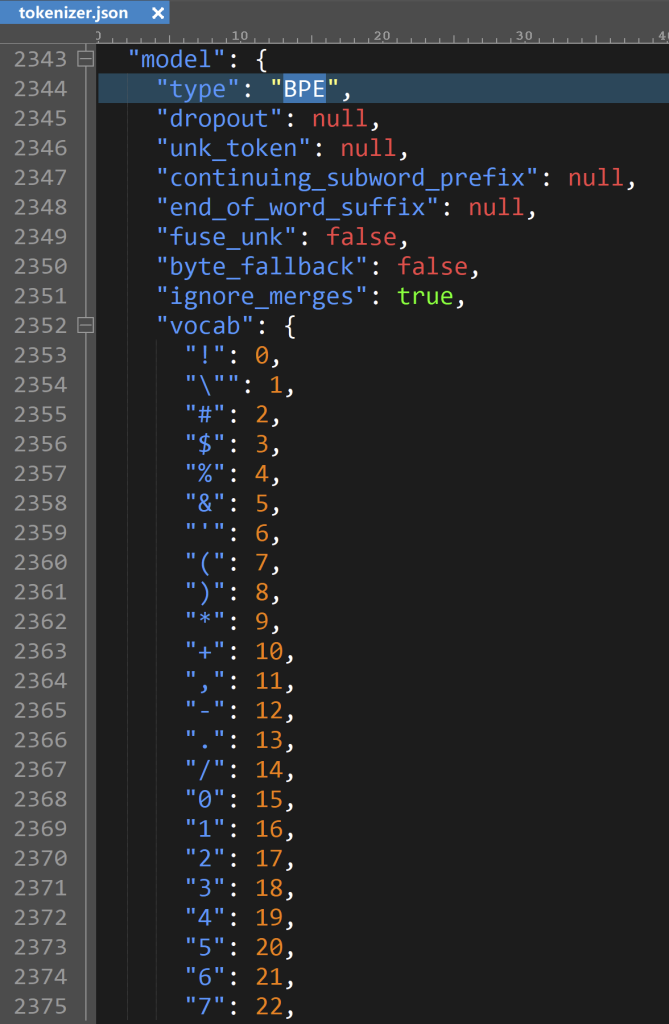
在文件 tokenizer.json 的前面还有其他特殊的 tokens
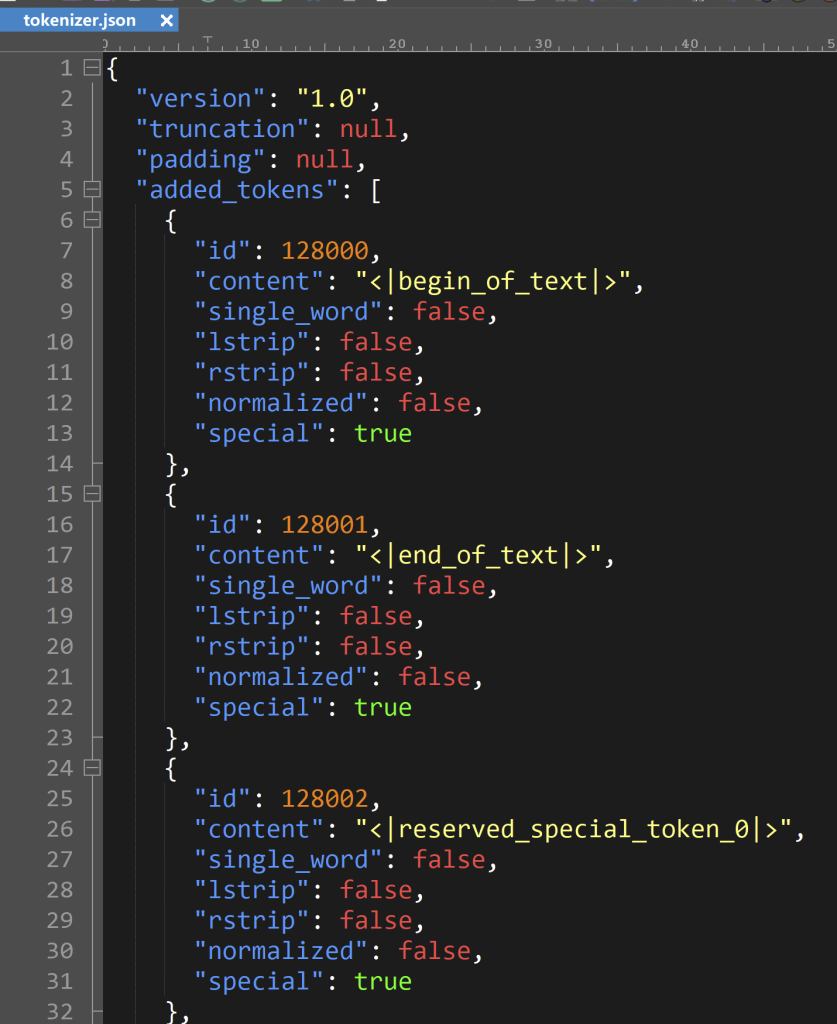
下面的代码含有了 tokenizer.json 文件里面所有特定的字符
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
from pathlib import Path import tiktoken from tiktoken.load import load_tiktoken_bpe import torch import json import matplotlib.pyplot as plt tokenizer_path = "Meta-Llama-3-8B/tokenizer.model" special_tokens = [ "<|begin_of_text|>", "<|end_of_text|>", "<|reserved_special_token_0|>", "<|reserved_special_token_1|>", "<|reserved_special_token_2|>", "<|reserved_special_token_3|>", "<|start_header_id|>", "<|end_header_id|>", "<|reserved_special_token_4|>", "<|eot_id|>", # end of turn ] + [f"<|reserved_special_token_{i}|>" for i in range(5, 256 - 5)] mergeable_ranks = load_tiktoken_bpe(tokenizer_path) tokenizer = tiktoken.Encoding( name=Path(tokenizer_path).name, pat_str=r"(?i:'s|'t|'re|'ve|'m|'ll|'d)|[^\r\n\p{L}\p{N}]?\p{L}+|\p{N}{1,3}| ?[^\s\p{L}\p{N}]+[\r\n]*|\s*[\r\n]+|\s+(?!\S)|\s+", mergeable_ranks=mergeable_ranks, special_tokens={token: len(mergeable_ranks) + i for i, token in enumerate(special_tokens)}, ) print(tokenizer.n_vocab) print(tokenizer.decode(tokenizer.encode("hello world!"))) |
运行结果:
|
1 2 |
128256 hello world! |
可以看到 tokenizer.n_vocab 的值为 128256,和 config.json 文件里的 vocab_size 一致
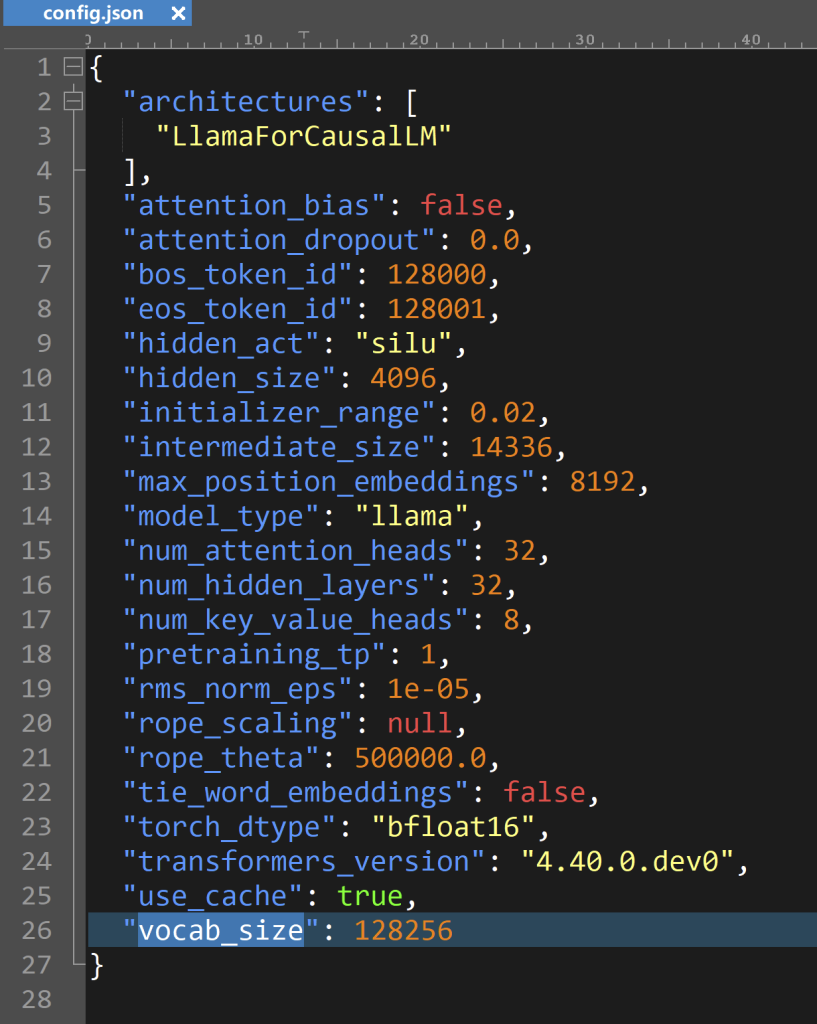
4. 读取模型文件
从头开始实现 llama3,我们将一次读取一个张量文件。
|
1 2 3 4 5 6 |
model = torch.load("Meta-Llama-3-8B/consolidated.00.pth") # Print the first 20 keys from the model dictionary print(json.dumps(list(model.keys())[:20], indent=4)) # Print the last two keys from the model dictionary print(json.dumps(list(model.keys())[-2:], indent=4)) |
运行结果:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
[ "tok_embeddings.weight", "layers.0.attention.wq.weight", "layers.0.attention.wk.weight", "layers.0.attention.wv.weight", "layers.0.attention.wo.weight", "layers.0.feed_forward.w1.weight", "layers.0.feed_forward.w3.weight", "layers.0.feed_forward.w2.weight", "layers.0.attention_norm.weight", "layers.0.ffn_norm.weight", "layers.1.attention.wq.weight", "layers.1.attention.wk.weight", "layers.1.attention.wv.weight", "layers.1.attention.wo.weight", "layers.1.feed_forward.w1.weight", "layers.1.feed_forward.w3.weight", "layers.1.feed_forward.w2.weight", "layers.1.attention_norm.weight", "layers.1.ffn_norm.weight", "layers.2.attention.wq.weight" ] [ "norm.weight", "output.weight" ] |
这些键名代表了模型中不同部件的参数。以下是对每个键的解释:
- tok_embeddings.weight – 代表词嵌入层的权重,它负责将输入的单词(或标记)转换为固定大小的向量。
- layers.x.attention.wq.weight, wk.weight, wv.weight, wo.weight – 这些分别表示在Transformer的第x层中,多头注意力(multi-head attention)机制的查询(Query)、键(Key)、值(Value)和输出(Output)的权重。
- layers.x.feed_forward.w1.weight, w2.weight, w3.weight – 这些代表在第x层的前馈神经网络(feed-forward network, FFN)中的不同权重。通常在BERT或Transformer模型中,FFN包含两个线性变换,这里w1和w2可能代表这两个变换的权重,w3可能是扩展实现的一部分。
- layers.x.attention_norm.weight, layers.x.ffn_norm.weight – 这些是应用在多头注意力和前馈神经网络输出上的层归一化(layer normalization)的权重。
- norm.weight – 这可能是模型最后的层归一化权重,用于整个模型输出的最终归一化处理。
- output.weight – 这是模型输出层的权重。
以上每个参数都在模型内部承担着重要的角色,确保信息能够在模型层间有效传递并进行适当的变换。
下面是查看其他模型参数:
|
1 2 3 |
with open("Meta-Llama-3-8B/params.json", "r") as f: config = json.load(f) config |
运行结果:
|
1 2 3 4 5 6 7 8 9 |
{'dim': 4096, 'n_layers': 32, 'n_heads': 32, 'n_kv_heads': 8, 'vocab_size': 128256, 'multiple_of': 1024, 'ffn_dim_multiplier': 1.3, 'norm_eps': 1e-05, 'rope_theta': 500000.0} |
这些参数是用于配置一个基于Transformer架构的神经网络模型的各种设置。每个参数的具体作用如下:
- dim: 表示模型中每层的维度或隐藏层的大小。在这里,它被设置为4096,意味着每个Transformer层的内部向量将有4096个维度。
- n_layers: 模型中的层数。这个参数值为32,意味着这个模型有32层Transformer层。
- n_heads: 多头注意力机制中头的数量。在这里,它是32,表示每个注意力层会有32个不同的头并行处理信息。
- n_kv_heads: 特定于某些模型的参数,可能表示在处理键(K)和值(V)时使用的注意力头的数量。在这个模型中,这个数值为8。
- vocab_size: 词汇表的大小,即模型可以识别的不同单词或标记的总数。这里设置为128,256。
- multiple_of: 这通常用于确保模型维度的一些方面(如层大小)是某个数值(1024)的倍数,这有助于优化计算效率。
- ffn_dim_multiplier: 前馈网络维度乘数。这里是1.3,意味着前馈层的内部维度是输入/输出维度(dim)的1.3倍,即计算为 (4096 \times 1.3).
- norm_eps: 层归一化操作中使用的一个极小数(epsilon),用于避免除以零的错误。这里设置为 (10^{-5})。
- rope_theta: 特定于某些Transformer模型的参数,可能与旋转位置编码(RoPE)有关。在这里,它设置为500000.0,这可能影响模型处理位置信息的方式。
这些参数共同定义了一个复杂的深度学习模型的结构和行为,每个都对模型的性能和能力产生重要影响。
保存这些参数
|
1 2 3 4 5 6 7 8 9 |
dim = config["dim"] n_layers = config["n_layers"] n_heads = config["n_heads"] n_kv_heads = config["n_kv_heads"] vocab_size = config["vocab_size"] multiple_of = config["multiple_of"] ffn_dim_multiplier = config["ffn_dim_multiplier"] norm_eps = config["norm_eps"] rope_theta = torch.tensor(config["rope_theta"]) |
这些行从config的字典中提取特定的模型配置参数。这包括模型的维度、层数、头的数量等,以及将rope_theta参数转换为一个PyTorch张量。
5. 将文本转换为标记
在这里,我们使用 tiktoken(我认为是 OpenAI 库)作为分词器
|
1 2 3 4 |
prompt = "the answer to the ultimate question of life, the universe, and everything is " tokens = [128000] + tokenizer.encode(prompt) print(tokens) print(len(tokens)) |
运行结果:
|
1 2 |
[128000, 1820, 4320, 311, 279, 17139, 3488, 315, 2324, 11, 279, 15861, 11, 323, 4395, 374, 220] 17 |
这里 128000,代表 bos_token_id,bos_token,”<|begin_of_text|>”
17 表示tokens 的长度。
这里定义了一个文本提示,并使用tokenizer.encode方法将其转换为标记。标记128000被添加到编码的标记列表的开头,可能代表某种特殊或起始标记。接着打印这些标记及其数量。
我们再从tokens 还原出来原来的内容:
|
1 2 3 |
tokens = torch.tensor(tokens) prompt_split_as_tokens = [tokenizer.decode([token.item()]) for token in tokens] print(prompt_split_as_tokens) |
运行结果:
|
1 |
['<|begin_of_text|>', 'the', ' answer', ' to', ' the', ' ultimate', ' question', ' of', ' life', ',', ' the', ' universe', ',', ' and', ' everything', ' is', ' '] |
将标记列表转换为PyTorch张量,然后迭代每个标记,将其解码回文本形式并打印。这是为了验证标记是否正确解码回其原始文本。
6. 将令牌转换为其嵌入
对不起,这是使用内置神经网络模块的代码库中唯一部分
无论如何,我们的 [17×1] 令牌现在是 [17×4096],即 17 个长度为 4096 的嵌入(每个令牌一个)
|
1 2 3 4 5 |
embedding_layer = torch.nn.Embedding(vocab_size, dim) embedding_layer.weight.data.copy_(model["tok_embeddings.weight"]) token_embeddings_unnormalized = embedding_layer(tokens).to(torch.bfloat16) token_embeddings_unnormalized.shape print(token_embeddings_unnormalized) |
运行结果:
|
1 |
torch.Size([17, 4096]) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
tensor([[-1.4305e-04, 1.0777e-04, -1.9646e-04, ..., 2.0218e-04, 1.4842e-05, 3.0136e-04], [ 1.4267e-03, -5.1575e-03, 2.0905e-03, ..., 1.0437e-02, -9.7656e-03, -7.8735e-03], [-1.1719e-02, 4.4861e-03, 1.1444e-03, ..., 9.0790e-04, 1.0681e-02, -6.7444e-03], ..., [-4.3945e-03, -6.2866e-03, 9.8877e-03, ..., 5.1575e-03, 2.3193e-03, -8.6212e-04], [-2.9144e-03, 1.5335e-03, -2.4605e-04, ..., 9.7046e-03, 4.2114e-03, 7.9956e-03], [-2.1172e-04, -1.5545e-04, 1.5945e-03, ..., -1.6632e-03, 1.1673e-03, -1.1826e-03]], dtype=torch.bfloat16, grad_fn=<ToCopyBackward0>) |
这部分代码创建了一个词嵌入层,其大小为vocab_size x dim。然后将预训练模型的词嵌入权重复制到这个新层的权重中。使用这个词嵌入层将输入的标记转换为嵌入向量,并将数据类型转换为bfloat16(一种用于深度学习中节省内存的浮点格式)。最后,打印嵌入向量的形状(shapes)和内容。
7. 使用 RMS 规范化对嵌入进行规范化
请注意,在此步骤之后,形状(shapes)不会改变,值只是归一化
要记住的事情,我们需要一个norm_eps(来自 config),因为我们不想意外地将 rms 设置为 0 并除以 0
公式如下:

|
1 2 3 4 5 |
# def rms_norm(tensor, norm_weights): # rms = (tensor.pow(2).mean(-1, keepdim=True) + norm_eps)**0.5 # return tensor * (norm_weights / rms) def rms_norm(tensor, norm_weights): return (tensor * torch.rsqrt(tensor.pow(2).mean(-1, keepdim=True) + norm_eps)) * norm_weights |
这个Python函数rms_norm是一个应用根均方(RMS)标准化技术来标准化张量的函数,并使用权重进行缩放。
函数rms_norm接受两个参数:
tensor:待标准化的张量。norm_weights:用于缩放标准化张量的权重张量。
标准化计算:
tensor.pow(2): 将张量中的每个元素平方。.mean(-1, keepdim=True): 计算这些平方值沿最后一个维度的平均值,并保持维度以便进行广播。+ norm_eps: 在平均值上加上一个小数(norm_eps),防止除零,这对于数值稳定性是必需的。torch.rsqrt(...): 计算这个结果的平方根的倒数。tensor * torch.rsqrt(...): 将原始张量乘以这个值进行标准化。... * norm_weights: 最后,用norm_weights缩放标准化后的张量。
整个操作确保了张量基于其最后一个维度上的RMS值被缩小,然后通过norm_weights进行调整,这可以用来实现一种参数化的标准化形式。
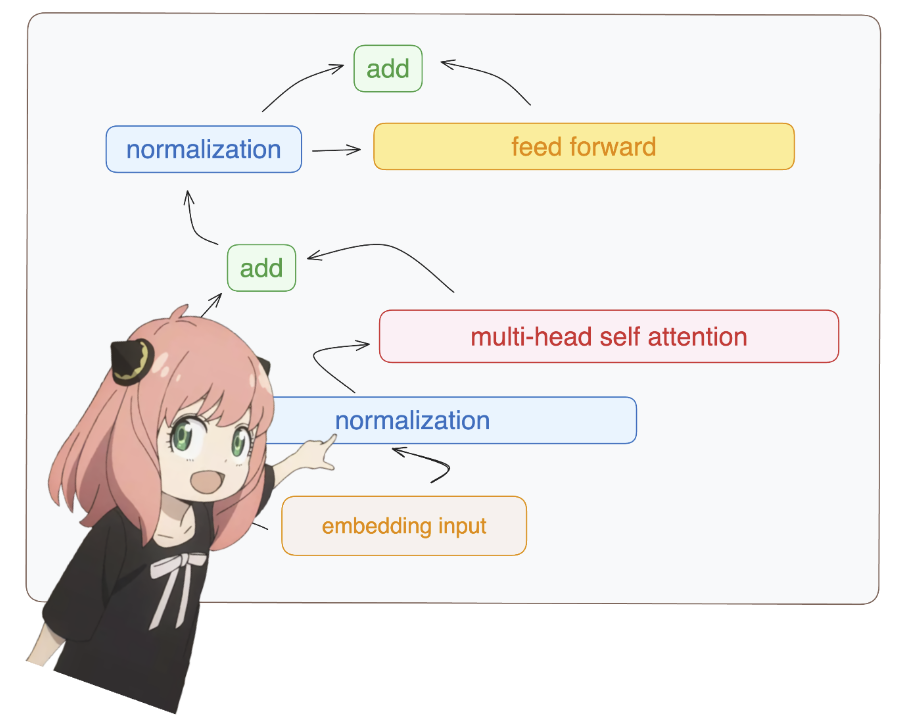
8. 构建变压器的第一层
8.1 规范化
您将看到我从模型字典访问 layer.0(这是第一层)
无论如何,在归一化后,我们的形状仍然 [17×4096] 与嵌入相同,但归一化
|
1 2 |
token_embeddings = rms_norm(token_embeddings_unnormalized, model["layers.0.attention_norm.weight"]) token_embeddings.shape |
运行结果:
|
1 |
torch.Size([17, 4096]) |
这行代码调用了之前定义的rms_norm函数,用于对token_embeddings_unnormalized(未标准化的token嵌入)进行标准化处理。标准化使用的权重是从模型中提取的,特定于第0层的注意力层的归一化权重(model["layers.0.attention_norm.weight"])。
这个函数将返回一个新的张量token_embeddings,其维度应与输入张量token_embeddings_unnormalized保持一致。因此,如果您问及token_embeddings.shape的值,它应该与token_embeddings_unnormalized的形状相同。具体形状取决于输入张量token_embeddings_unnormalized的维度,通常在处理NLP任务时,这个张量的形状为(batch_size, sequence_length, embedding_dim),其中embedding_dim是在前面定义的dim。
8.2 注意头从头开始实现
让我们加载变压器第一层的注意头
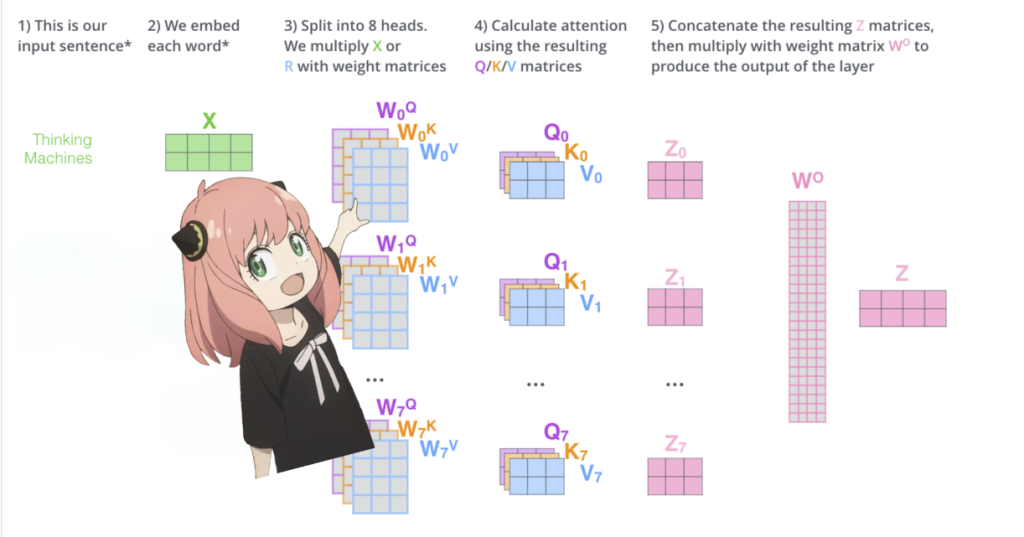
当我们从模型中加载查询(query)、键(key)、值(value)和输出(output)向量时,我们注意到它们的形状分别是 [4096×4096]、[1024×4096]、[1024×4096] 和 [4096×4096]。乍一看这很奇怪,因为理想情况下我们希望每个头分别有自己的q、k、v和o。
代码的作者将它们捆绑在一起,因为这样做很方便,有助于并行化注意力头的乘法运算。
我将解开所有这些…
|
1 2 3 4 5 6 |
print( model["layers.0.attention.wq.weight"].shape, model["layers.0.attention.wk.weight"].shape, model["layers.0.attention.wv.weight"].shape, model["layers.0.attention.wo.weight"].shape ) |
运行结果:
|
1 |
torch.Size([4096, 4096]) torch.Size([1024, 4096]) torch.Size([1024, 4096]) torch.Size([4096, 4096]) |
8.3 解包查询
在下一节中,我们将解包来自多个注意力头的查询,生成的形状为 [32x128x4096]
这里,32 是 llama3 中的注意力头数,128 是查询向量的大小,4096 是令牌嵌入的大小
|
1 2 3 4 5 6 7 8 9 |
# 从模型中获取第0层的查询权重 q_layer0 = model["layers.0.attention.wq.weight"] # 计算每个头的维度,总维度除以头的数量 head_dim = q_layer0.shape[0] // n_heads # 将查询权重重塑为多头格式(头数, 头维度, 总维度) q_layer0 = q_layer0.view(n_heads, head_dim, dim) q_layer0.shape head_dim |
运行结果:
|
1 2 |
torch.Size([32, 128, 4096]) head_dim |
9. 实现第一层的第一个头
这里我访问查询权重矩阵第一层的第一头,这个查询权重矩阵的大小是[128×4096]
|
1 2 3 4 5 |
# 提取第0个头的查询权重 q_layer0_head0 = q_layer0[0] q_layer0_head0.shape |
运行结果:
|
1 |
torch.Size([128, 4096]) |
10. 将查询权重与令牌嵌入相乘,以接收对令牌的查询
在这里,您可以看到生成的形状是 [17×128],这是因为我们有 17 个标记,每个标记都有一个 128 长度的查询。
|
1 2 3 4 |
# 对每个标记的嵌入使用第0个头的查询权重进行矩阵乘法,得到每个标记对应的查询表示 q_per_token = torch.matmul(token_embeddings, q_layer0_head0.T) q_per_token.shape |
运行结果:
|
1 |
torch.Size([17, 128]) |
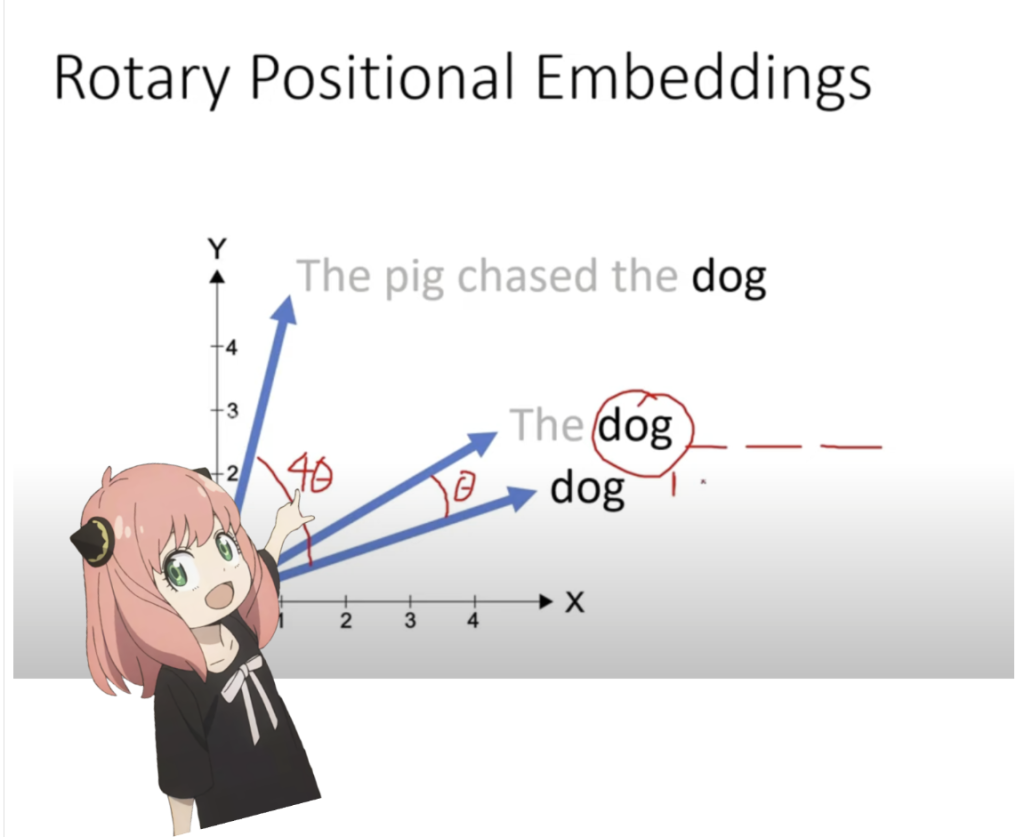
11. 定位编码
我们现在正处于一个阶段,我们在提示中为每个标记都有一个查询向量,但如果你仔细想想,个性化查询向量不知道提示中的位置。
查询:“生命、宇宙和万物的终极问题的答案是”
在我们的提示中,我们已经使用了 “the” 三次,我们需要所有 3 个 “the” 标记的查询向量根据它们在查询中的位置具有不同的查询向量(每个大小为 [1×128])。我们使用 RoPE(旋转位置嵌入)执行这些旋转。
RoPE
观看此视频(这是我观看的)以了解数学。 https://www.youtube.com/watch?v=o29P0Kpobz0&t=530s
|
1 2 |
q_per_token_split_into_pairs = q_per_token.float().view(q_per_token.shape[0], -1, 2) q_per_token_split_into_pairs.shape |
运行结果:
|
1 |
torch.Size([17, 64, 2]) |
在上面的步骤中,我们将查询向量拆分为对,我们对每对应用旋转角度偏移!
我们现在有一个大小为 [17x64x2] 的向量,这是提示中每个标记的 128 个长度查询,分为 64 对!这 64 对中的每一对都将由 m*(theta) 旋转,其中 m 是我们旋转查询的令牌的位置!
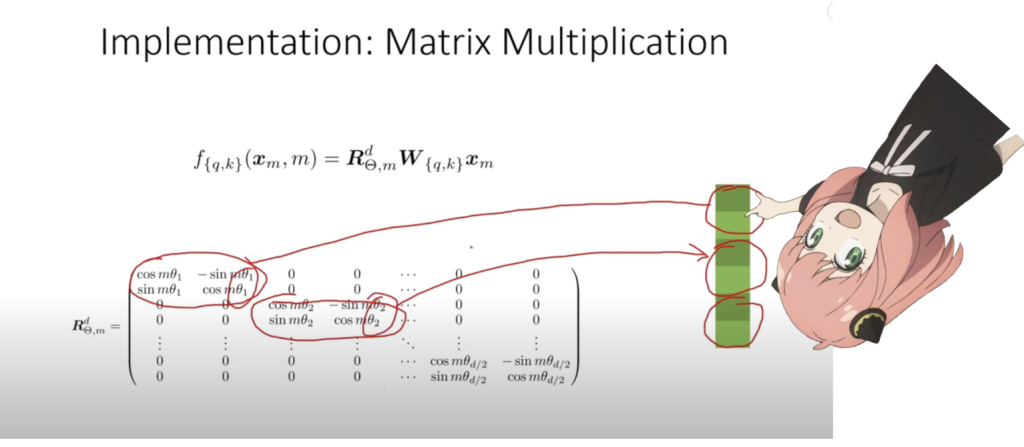
关于 q_per_token_split_into_pairs.shape 的中文解释:
这段代码首先将q_per_token张量的数据类型转换为浮点型,然后调用view方法来改变张量的形状。具体的变形操作是保持第一个维度(通常是批处理大小)不变,第三个维度设置为 2,这意味着每两个元素被分为一组,而第二个维度使用 -1 自动计算,以确保元素总数保持不变。这样操作通常用于准备数据以适配某些特定的处理需求,例如在某些神经网络操作中需要成对处理数据。
最终得到的 q_per_token_split_into_pairs 的形状会是一个三维张量,其中:
- 第一维度是原张量的第一维度(如批次大小)。
- 第二维度是自动计算出的,确保所有元素都被恰当地分配到大小为2的小组中。
- 第三维度固定为2,表示分组的大小。
这样的变形操作对于进一步处理数据,如在处理双向关系或成对特征时,非常有用。
12. 使用复数的点积旋转向量
|
1 2 |
zero_to_one_split_into_64_parts = torch.tensor(range(64))/64 zero_to_one_split_into_64_parts |
|
1 |
tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250,<br> 0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656,<br> 0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062,<br> 0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469,<br> 0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875,<br> 0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281,<br> 0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688,<br> 0.9844])<br> |
这段代码创建了一个从0到1均匀分成64部分的张量。具体解释如下:
- 创建序列:
range(64)生成了一个从0到63的整数序列。 - 转换为张量:
torch.tensor(range(64))将这个序列转换成了一个PyTorch张量。 - 除以64:
.../64操作将张量中的每个元素除以64,因此元素的值从0开始(0/64),以1/64为步长,最终到达63/64,不包括1(因为是从0开始的64个数,最大数为63)。
所得到的张量zero_to_one_split_into_64_parts包含64个浮点数,这些数值均匀地分布在0到1之间(不包括1)。这样的数据常用于生成需要等间距数值的场合,例如在某些图形渲染、数据标准化或机器学习模型输入预处理中。
|
1 2 3 4 5 |
# 创建一个频率数组。这里,zero_to_one_split_into_64_parts 包含从0到1(不包括1)均匀分布的64个数值。 # 这些数值被用来计算幂函数 rope_theta 的幂次,然后取倒数,得到相应的频率。 # rope_theta 通常用于调整周期性编码的尺度,此处的操作是将其调整到一个特定的频率范围内。 freqs = 1.0 / (rope_theta ** zero_to_one_split_into_64_parts) freqs |
在这段代码中:
rope_theta是一个预定义的标量,用于调整生成频率的尺度。zero_to_one_split_into_64_parts是一个从0增加到接近1的64个值的数组,每个数值都等间隔分布。rope_theta ** zero_to_one_split_into_64_parts计算了rope_theta的各个幂次,幂的底数是rope_theta,指数是zero_to_one_split_into_64_parts中的值。这样可以生成一系列经过非线性变换的尺度。- 取倒数(
1.0 / ...)将这些幂次转换成对应的频率值,这些频率通常用于某些周期性编码过程,如在某些类型的神经网络(尤其是那些处理时间序列数据的)中。
freqs张量包含了根据rope_theta和均匀间隔的指数值调整后的一系列频率。这些频率可用于进一步的数据处理或特征工程,特别是在处理与周期性或波形相关的任务时。
运行结果:
|
1 2 3 4 5 6 7 8 9 10 11 |
tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01, 2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01, 8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02, 2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03, 7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03, 2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04, 6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04, 1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05, 5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05, 1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06, 4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06]) |
|
1 2 3 4 5 6 7 8 9 10 |
# 计算每个标记对应的频率。使用torch.outer函数创建一个外积矩阵,行数为17,列使用前面计算的频率freqs。 # 这样,每个标记都会有对应的一组频率值。 freqs_for_each_token = torch.outer(torch.arange(17), freqs) # 使用torch.polar将频率转换为复数形式。torch.polar接收幅值(这里为1,表示单位圆上的点)和相位(频率),输出相应的复数。 # 这里每个频率值被转换成了复平面上的一个点。 freqs_cis = torch.polar(torch.ones_like(freqs_for_each_token), freqs_for_each_token) # 打印freqs_cis张量的形状,它应该是一个二维张量,其中的每个元素都是一个复数。 freqs_cis.shape |
运行结果:
|
1 |
torch.Size([17, 64]) |
|
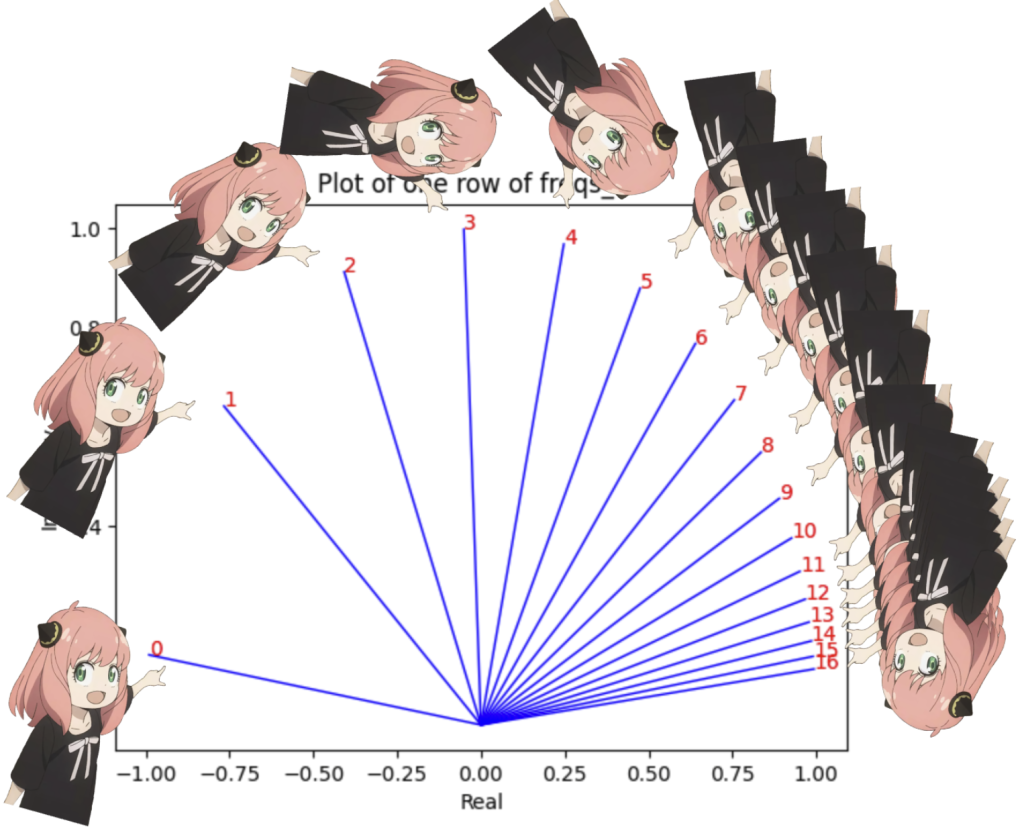
1 2 3 4 5 6 7 8 9 10 11 12 |
# 查看freqs_cis的第三行,即第三个标记对应的所有复数频率。 value = freqs_cis[3] # 使用matplotlib绘图展示这一行的复数频率。绘制从原点到每个复数点的线,并在每个点处标注索引。 plt.figure() for i, element in enumerate(value[:17]): plt.plot([0, element.real], [0, element.imag], color='blue', linewidth=1, label=f"Index: {i}") plt.annotate(f"{i}", xy=(element.real, element.imag), color='red') plt.xlabel('Real') plt.ylabel('Imaginary') plt.title('Plot of one row of freqs_cis') plt.show() |
运行结果:
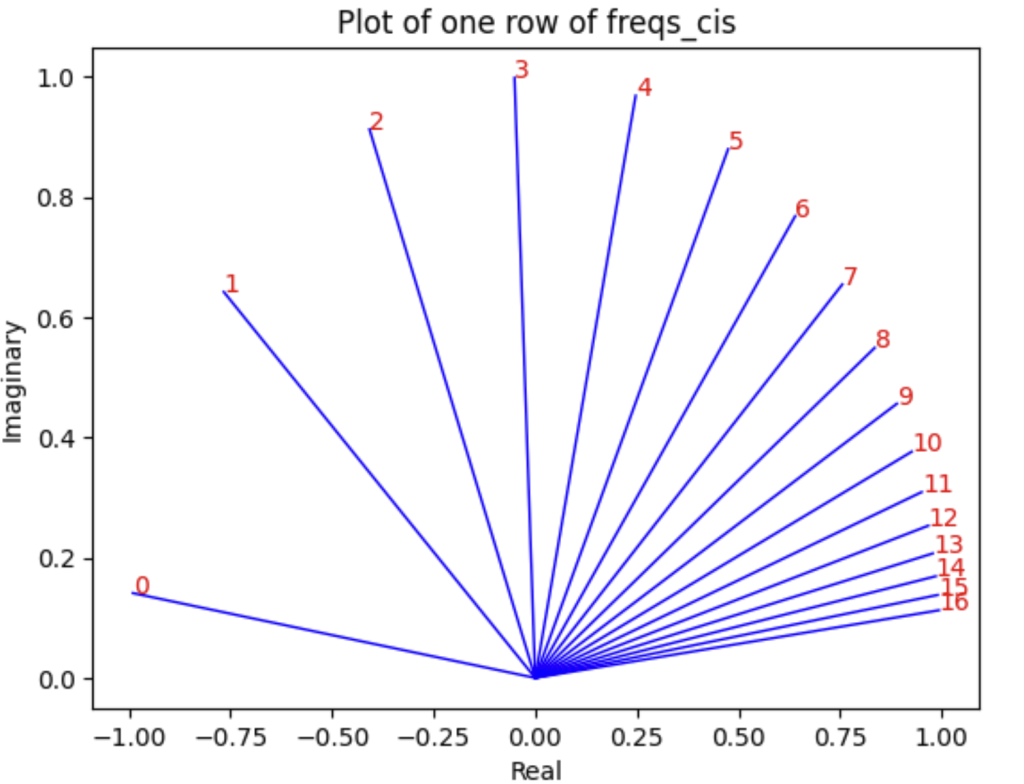
这段代码首先使用torch.outer计算17个标记每个对应的频率集合。然后,使用torch.polar函数将这些频率转换为复数表示,其中实部和虚部分别对应复平面上的横坐标和纵坐标。最后,使用matplotlib绘图库在复平面上绘制出这些复数点,并通过直线将它们与原点相连,形象地展示了这些复数的分布和相位变化。这可以用于可视化分析频率分布的特性,尤其是在处理涉及信号处理或周期性数据的场景中。
13. 有了每个令牌的查询元素的复数(角度变化向量)
我们可以将查询(我们分成对的查询)转换为复数,然后点积根据位置旋转查询
|
1 2 3 |
# 将成对的实数张量转换为复数张量,每对实数对应一个复数(第一个是实部,第二个是虚部) q_per_token_as_complex_numbers = torch.view_as_complex(q_per_token_split_into_pairs) q_per_token_as_complex_numbers.shape |
运行结果:
|
1 |
torch.Size([17, 64]) |
在这段代码中:
torch.view_as_complex(q_per_token_split_into_pairs):该函数将输入的实数张量视为复数张量,其中输入张量的最后一个维度大小必须是2,分别代表复数的实部和虚部。
对于张量形状的解释:
- 假设
q_per_token_split_into_pairs的形状是(batch_size, sequence_length, 2),其中2表示成对的实部和虚部。 - 使用
torch.view_as_complex后,最后一个维度会被视为复数的一部分,因此新的张量q_per_token_as_complex_numbers的形状将变为(batch_size, sequence_length),每个元素都是一个复数。
这种转换通常用于信号处理或神经网络中处理复数数据,使得后续的计算可以直接在复数域中进行。
|
1 2 |
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cis q_per_token_as_complex_numbers_rotated.shape |
运行结果:
|
1 |
torch.Size([17, 64]) |
q_per_token_as_complex_numbers * freqs_cis:这个操作将两个复数张量相乘。在复数乘法中,两个复数相乘的结果是一个新的复数,其模长是原两个复数模长的乘积,其角度是原两个复数角度的和。
对于张量形状的解释:
- 假设
q_per_token_as_complex_numbers的形状是(batch_size, sequence_length),其中每个元素是一个复数。 freqs_cis的形状应当与q_per_token_as_complex_numbers兼容,例如也是(batch_size, sequence_length)或能够广播到这个形状。- 结果张量
q_per_token_as_complex_numbers_rotated将保持与q_per_token_as_complex_numbers相同的形状(batch_size, sequence_length)。
这样的操作常用于信号处理和深度学习中的特征变换,尤其是在处理需要调整相位或频率特性的应用中。每个复数的旋转可以看作是在复平面上的一个角度变化,这对于某些类型的算法(比如那些涉及时间序列或周期性数据处理的算法)特别有用。
14. 获得旋转向量后
我们可以通过再次将复数视为实数来将查询作为对返回
|
1 2 |
q_per_token_split_into_pairs_rotated = torch.view_as_real(q_per_token_as_complex_numbers_rotated) q_per_token_split_into_pairs_rotated.shape |
运行结果:
|
1 |
torch.Size([17, 64, 2]) |
这个操作的具体行为如下:
torch.view_as_real(q_per_token_as_complex_numbers_rotated):此函数将输入的复数张量转换为实数张量,每个复数的实部和虚部成对出现,形成最后一个维度的两个连续元素。
关于张量形状的解释:
- 假设
q_per_token_as_complex_numbers_rotated的形状是(batch_size, sequence_length),其中每个元素是一个复数。 - 转换后的张量
q_per_token_split_into_pairs_rotated的形状将变为(batch_size, sequence_length, 2)。最后的2表示复数的两个组成部分:实部和虚部。
这样的转换使得复数数据的实部和虚部可以作为独立的特征在后续处理中使用,适用于需要分别处理复数实部和虚部的场景,例如在某些机器学习模型的输入处理中。
旋转后的对现在已经合并,我们现在有了一个新的查询向量(旋转后的查询向量),其形状为 [17×128],其中 17 是标记的数量,128 是查询向量的维度。
|
1 2 |
q_per_token_rotated = q_per_token_split_into_pairs_rotated.view(q_per_token.shape) q_per_token_rotated.shape |
运行结果:
|
1 |
torch.Size([17, 128]) |
在这里:
q_per_token.shape原本的形状可能是(batch_size, sequence_length),假设之前操作中每个token对应的复数(实部和虚部)被视为独立的特征或维度处理。view(q_per_token.shape)方法用于将张量q_per_token_split_into_pairs_rotated从包含复数实虚部的三维形状(batch_size, sequence_length, 2)转换回二维形状(batch_size, sequence_length)。这种操作通常意味着在某种处理(如复数到实数的转换)之后,我们需要恢复数据到某个特定的维度结构以适配后续的处理流程。
因此,最终的张量 q_per_token_rotated 将保持与原始 q_per_token 相同的形状,这也意味着每个 token 现在对应一个合并后的特征向量,而不再是分开的实部和虚部。
15. 键(几乎与查询相同)
不打算通过钥匙的数学计算,你唯一需要记住的是:
键生成键向量,也是 dimention 128
键的权重数只有查询权重的 1/4,这是因为键的权重一次在 4 个头之间共享,以减少所需的计算次数
键也会旋转以添加位置信息,就像出于相同原因的查询一样
|
1 2 3 4 5 6 7 8 |
# 从模型中获取第0层的键(key)权重 k_layer0 = model["layers.0.attention.wk.weight"] # 将键(key)权重矩阵重新形状为 (n_kv_heads, k_layer0.shape[0] // n_kv_heads, dim) # 其中 n_kv_heads 是键向量的头数,dim 是每个头的维度 k_layer0 = k_layer0.view(n_kv_heads, k_layer0.shape[0] // n_kv_heads, dim) k_layer0.shape |
运行结果:
|
1 |
torch.Size([8, 128, 4096]) |
n_kv_heads表示用于键向量的头的数量。k_layer0.shape[0] // n_kv_heads计算每个头需要处理的键向量的数量。dim是每个键向量的维度,通常与模型的嵌入维度相匹配。
该操作后的 k_layer0 的形状将是 (n_kv_heads, k_layer0.shape[0] // n_kv_heads, dim)。这意味着:
- 第一维
n_kv_heads表示头的数量。 - 第二维
k_layer0.shape[0] // n_kv_heads表示每个头处理的键向量的数量。 - 第三维
dim表示每个键向量的维度。
这种重塑是为了便于在后续操作中,每个注意力头能够独立地对应并处理其分配的键向量,从而实现有效的并行处理和更精细的注意力机制。
|
1 2 |
k_layer0_head0 = k_layer0[0] k_layer0_head0.shape |
运行结果:
|
1 |
torch.Size([128, 4096]) |
|
1 2 |
k_per_token = torch.matmul(token_embeddings, k_layer0_head0.T) k_per_token.shape |
运行结果:
|
1 |
torch.Size([17, 128]) |
|
1 2 |
k_per_token_split_into_pairs = k_per_token.float().view(k_per_token.shape[0], -1, 2) k_per_token_split_into_pairs.shape |
运行结果:
|
1 |
torch.Size([17, 64, 2]) |
|
1 2 |
k_per_token_as_complex_numbers = torch.view_as_complex(k_per_token_split_into_pairs) k_per_token_as_complex_numbers.shape |
运行结果:
|
1 |
torch.Size([17, 64]) |
|
1 2 |
k_per_token_split_into_pairs_rotated = torch.view_as_real(k_per_token_as_complex_numbers * freqs_cis) k_per_token_split_into_pairs_rotated.shape |
运行结果:
|
1 |
torch.Size([17, 64, 2]) |
|
1 2 |
k_per_token_rotated = k_per_token_split_into_pairs_rotated.view(k_per_token.shape) k_per_token_rotated.shape |
|
1 |
torch.Size([17, 128]) |